간단한 예시를 이용한 분류모델 성능지표 알아보기

공대생 배기웅 2023. 7. 6. 17:42

Confusion Matrix (혼동행렬)

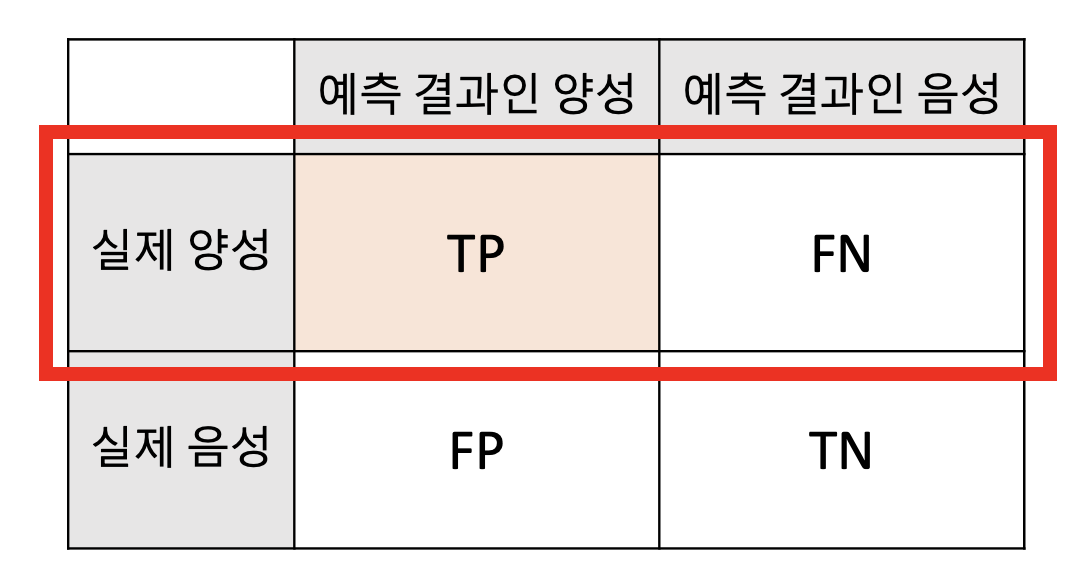
- 학습을 통한 예측성능을 측정하기 위해 예측값과 실제값을 비교하기 위한 표

	예측한 양성 값	예측한 음성 값
실제 양성 값	TP (True Positive)	FN (False Negative)
실제 음성 값	FP (False Positive)	TP (True Positive)

error rate (오차율)

- $\frac{FN+FP}{Total}$

accuracy (정확도)

- $\frac{TP + TN}{Total}$

Precision (정밀도)

- 모델이 양성이라고 분류한 것들 중, 실제 값이 양성인 비율

- 모델이 정확하게 양성으로 예측했는지를 나타내는 지표

- 거짓양성 (FP)를 최소화하는데 초점을 맞춘다.

- $\frac{TP}{TP + FP}$

Recall (재현도)

- 실제 양성 값들 중, 모델이 양성이라고 예측한 것들의 비율

- 모델이 양성인 것들을 얼마나 잘 찾아내는지를 나타내는 지표

- 거짓음성 (FN)을 최소화하는데 초점을 맞춘다.

- $\frac{TP}{TP + FN}$

F1-score

- 정밀도와 재현도의 조화평균

- F1 스코어는 데이터의 분포가 불균형할 때 사용하는 지표이다.

- F1 스코어를 통해 모델이 양성 클래스에 대해 일반적인 정확도만을 고려하는 것보다, 실제 양성 클래스를 더 잘 식별하는지를 평가할 수 있다.

- $2 \frac{PRE*REC}{PRE+REC}$

예시

아래와 같이 실제값과 예측값이 분포되어있다고 가정한다. 이 때, 1은 양성이고 0은 음성이라고 가정한다.

actual = [0,1,1,1,1,0,0,1,1,1]
predicted = [1,0,0,1,1,1,0,1,1,0]

위의 예시는 다음과 같은 Confusion Matrix로 표현할 수 있다.

python 소스코드를 통해 평가지표를 구한다.

actual = [0,1,1,1,1,0,0,1,1,1]
predicted = [1,0,0,1,1,1,0,1,1,0]

TP,FN,FP,TN = 0,0,0,0

for i in range(len(actual)):
  if predicted[i]==1: # TP or FP
    if predicted[i] == actual[i]:
      TP +=1
    else:
      FP +=1
  elif predicted[i] == 0: # TN or FN
    if predicted[i] == actual[i]:
      TN +=1
    else:
      FN +=1    
PRE = round(TP/(TP+FP),2)
REC = round(TP/(TP+FN),2)
print("TP : {} | FN : {}".format(TP, FN))
print("FP : {} | TN : {}".format(FP, TN))
print("정확도(Accuracy)는 {}/{}={}".format(TP,TP+FN+FP+TN, (TP+TN)/(TP+FN+FP+TN)))
print("정밀도(Precision)는 {}/{} = {}입니다.".format(TP, TP + FP, PRE))
print("재현도(Recall)는 {}/{} = {}입니다.".format(TP, TP + FN, REC))
print("F1-score는 2*({}*{})/({}+{}) = {}".format(PRE,REC,PRE,REC,round(2*(PRE*REC/(PRE+REC)),2)))

결과를 통해 단순 정확도는 50%가 나오는 반면, F1-score는 62%가 나옴을 알 수 있다.

Receiver Operating Characteristic (ROC)

- ROC-AUC 곡선은 다양한 임계값에서 모델의 분류 성능에 대한 측정 그래프임.

- ROC : 모든 임계값에서 분류 모델의 성능을 보여주는 그래프

- AUC : ROC 곡선 아래의 영역

- 우수한 모델은 AUC가 1에 가깝고, 불량한 모델은 AUC가 0에 가깝다. 실제로 AUC의 최소값은 0.5로, 이 경우는 모델의 분류 능력이 최악임을 나타냄.

ROC-AUC 곡선은 2개의 지표(민감도, 특이도)로 이루어진다.

- 민감도 : 실제 양성이었을 때, 예측 결과가 양성인 경우, $\frac{TP}{TP+FN}$로 표현되며 재현도와 동일하다.

- 특이도 : 실제 음성이었을 때, 예측 결과가 음성인 경우, $\frac{TN}{TN+FP}$으로 표현된다.

- 모든 경우의 합은 일정하므로, 민감도와 특이도는 서로 반비례한다.

ROC-AUC 그래프의 x축은 (1-특이도) = FPR 값으로 나타내며, y축은 민감도 = TPR 값으로 나타낸다. 특이도와 TPR은 반비례하므로, FPR과 TPR은 서로 비례하는 방향으로 그래프가 그려진다.

왜 TPR과 FPR로 축을 설정하는가?

: 우선, 민감도는 "모델이 양성인 것들을 얼마나 잘 분류하는가?"를 확인하는 지표이며, 특이도는 "모델이 음성인 것들을 얼마나 잘 분류하는가?"를 확인하는 지표이다. 두 지표를 통해 양성인 것을 양성으로, 음성인 것을 음성으로 얼마나 잘 분류하는가를 동시에 확인할 수 있으며, 이를 비례적으로 시각화하기 위해 특이도 대신 FPR를 사용한다.

TPR과 FPR은 서로 보완적인 성격을 가지기 때문에 모델의 양성클래스 감지 능력과 음성클래스 감지 능력을 동시에 평가할 수 있다.

(i) AUC = 1인 경우

- 두 개의 곡선이 겹치지 않는 이상적인 상황이다.

- 양성 클래스와 음성클래스를 완벽하게 구별할 수 있다.