출처 => https://www.acmicpc.net/problem/2667
문제

사고의 흐름
▶ 전형적인 깊이우선탐색 알고리즘을 이용한 문제이다.
▶ 크게 2가지의 포인트를 잡아야 한다.
>> 첫 번째 포인트! 1이 발견되면 그 점을 중심으로 왼쪽 오른쪽 위 아래를 조사하는 것.
▶ 나의 풀이에서는 dx[]와 dy[] 배열을 이용하였다. 주위에 있는 x좌표와 y좌표를 nx와 ny로 설정하고 nx=x+dx[i] ny=y+dy[i]로 선언한다. i가 증가할 때마다 x와 y에 값을 더해준다.
▶ 여기서 중요한 것은 아래의 소스코드처럼 i번째의 숫자는 dx[i]와 dy[i]가 달라야 한다. 만약 0으로 같거나 1,-1로 둘이 같게 된다면 이동하지 않거나 대각선으로 이동하기 때문이다. dfs에서의 움직이는 방향은 수직, 수평 방향이다.
>> 두 번째 포인트! 1을 중심으로 dfs를 한 뒤에는 중심이 되는 그 점을 0으로 바꾸어 준다.
▶ cnt[k] 배열은 k번째 굴의 크기를 나타낸다. 위의 문제에서 1번째 굴의 크기는 7이다. 굴의 크기를 세는 원리는 dfs를 통해 주위에 1이 있으면 값을 1 더해주는 것이다.
▶ 그런데 중심이 되었던 점이 1로 유지가 된다면 그 옆의 점을 중심으로 dfs를 실행하였을 때 중복이 되는 문제가 생긴다. 따라서 중심으로 사용한 점은 0으로 변경해야 한다.
소스코드 및 실행결과
#include<iostream>
#include<algorithm>
using namespace std;
const int dx[] = { 0,0,-1,1 };
//dfs 실행시 x좌표의 움직임
const int dy[] = { -1,1,0,0 };
//dfs 실행시 y좌표이 움직임
//dx와 dy는 0과 1,-1이 겹치지 말아야 위아래 옆으로 움직이므로
int n;//지도의 옆면
int k;//굴의 개수
int cnt[101];//i번째 굴의 크기
int arr[101][101];//지도의 모습
void dfs(int x, int y) {
//dfs는 1인 위치를 중심으로 실행하므로 arr[x][y]=1이다.
arr[x][y] = 0, cnt[k]++;
//1이었던 것을 0으로 변경하고 cnt[k]에 1을 추가한다.
//1으로 바꾸는 것은 그 옆에 있는 것으로 dfs를 할 때 중복해서 세어지는 것을 막기 위해서이다.
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
//깊이우선탐색
if (arr[nx][ny] == 1) dfs(nx, ny);
//만약 1이라면 또다시 dfs를 실행!
}
}
void main() {
cin >> n;
//지도의 크기 입력
for (int i = 1; i <= n; i++)
for(int j=1;j<=n;j++)
cin >> arr[i][j];
//지도 입력
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (arr[i][j] == 1)
dfs(i, j), k++;
//만약 1이라면(굴이라면)이를 중심으로 dfs 실행
std::sort(cnt, cnt + k);
//cnt 배열을 작은 순으로 부터 오름차순으로 정렬
cout << k << endl;
//굴의 개수 출력
for (int i = 0; i < k; i++)
cout << cnt[i] << endl;
//각각의 굴의 크기 출력
}
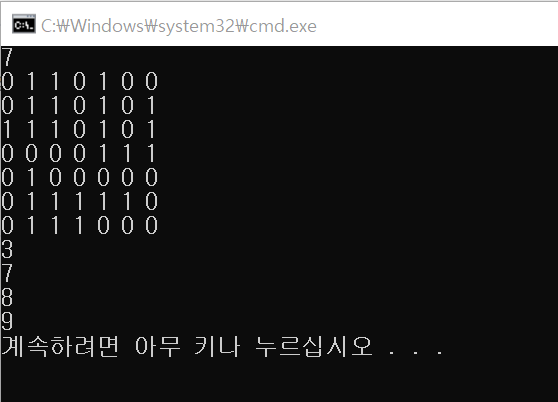
의견 및 반성
▶ 깊이우선탐색을 원리로만 알았지만 직접 적용을 하지 못했다. 적용이나 응용에서 부족한게 아니라 기초가 부족한 것이었으므로 많이 문제를 풀어봐야겠다.
'🖥️ 컴퓨터공학 🖥️ > 알고리즘' 카테고리의 다른 글
| [백준 - 1920] 수 찾기(feat. 이진탐색 알고리즘) / C++ (0) | 2020.07.04 |
|---|---|
| [백준 - 2178] 미로 탐색 (feat. 너비우선탐색) / C++ (0) | 2020.07.03 |
| [acmicpc] 두더지 굴 (feat. 깊이우선탐색 알고리즘) / C++ (0) | 2020.06.09 |
| [acmicpc] upper bound (feat. 이진 검색 알고리즘) / C++ (0) | 2020.06.08 |
| 백준) 2 x n 타일링 (재귀함수) / JAVA (0) | 2020.04.17 |