▶ 선형 회귀(Linear Regression)이란 무엇일까
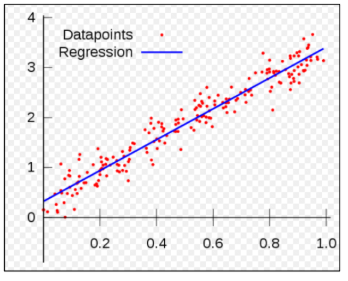
위의 그림을 보면 데이터 값을 나타내는 점(Datapoints)들과, 이 점들을 가로지르는 직선(Regression)이 존재한다. 회귀분석은 가장 합리적인 직선을 찾는 방법이다. 관측 값을 가장 잘 지나가는 직선 혹은 곡선의 방정식을 구하는 방법론을 우리는 회귀 분석이라고 한다. 그리고 직선을 구하는 분석을 선형회귀 분석이라고 한다. 이번 시간에는 선형회귀 분석에 대하여 알아보고자 한다.
이차원 좌표 평면에 다음과 같은 점들을 만족시키는 일차 함수가 있다고 가정해보자.
(1,3) (2,5) (3,7)
이 함수에 4를 넣으면 어떤 값이 출력될까?
직관적으로 우리는 답이 9라는 것을 안다. 함숫값이 3, 5, 7 순으로 공차가 2이고 첫 항이 3이기 때문에 9라는 답을 알 수 도 있었으나 y=2x+1이라는 그래프를 그려서 답을 알 수도 있을 것이다.
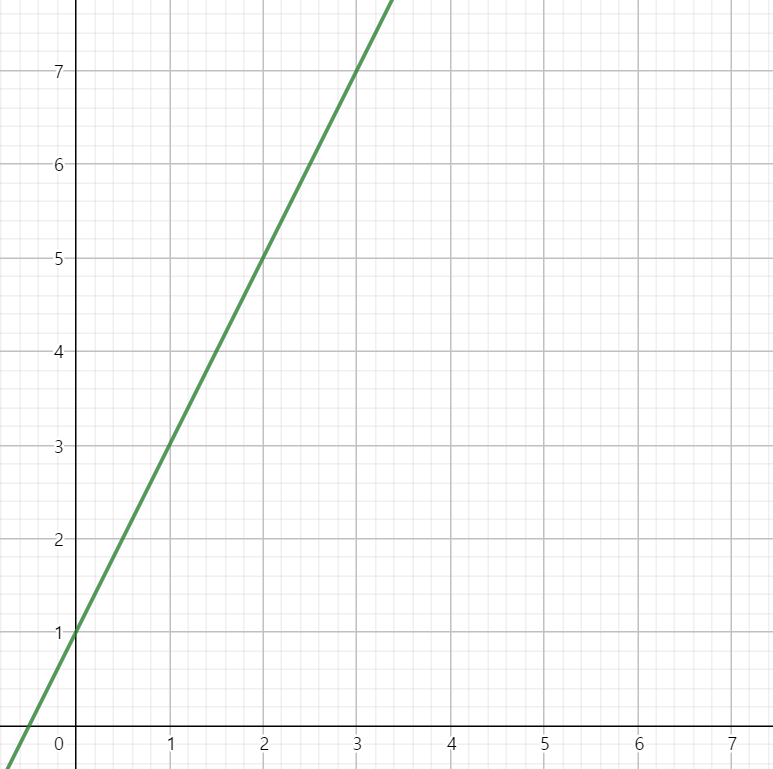
우리는 이 과정을 쉽게 구현할 수 있지만 컴퓨터는 그렇지 못하다. 따라서 선형회귀 분석법을 이용하여 컴퓨터가 y=2x+1이라는 그래프를 구현해 낼 수 있도록 도와주어야 한다.
▶ 문제의 원인을 분석한다, 손실함수와 최소 제곱법
위의 예시를 다시 한번 보자. 이차원 좌표 평면에는 (1,3) (2,5) (3,7)의 세점이 있다. 우리는 선형회귀 분석을 통해 이 세점들을 지나는 가장 바람직한 직선을 찾을 것이다. 즉, H(w,b)=wx+b라는 그래프에서 적절한 w와 b를 찾는 것이 목표이다.
임의로 초기값을 설정해준다. 가장 무난하게 w=1, b=0으로 초기값 설정을 해보자.
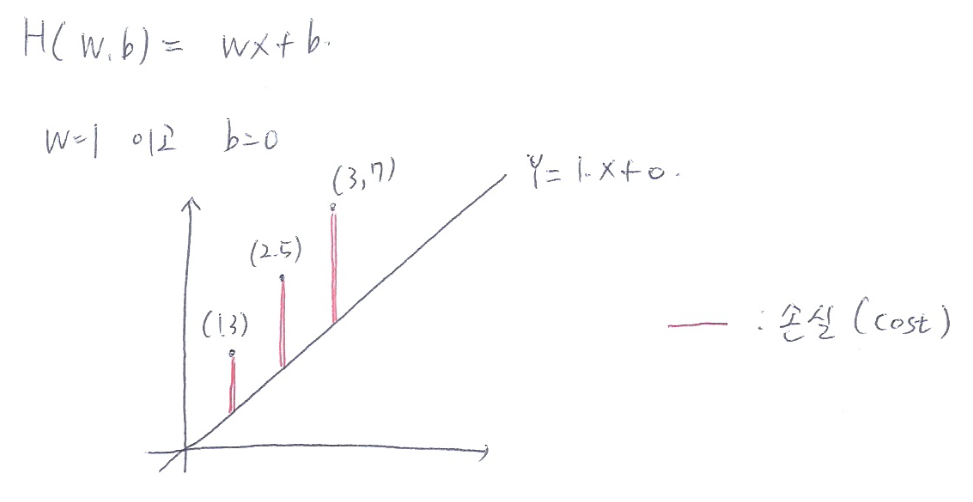
위와 같이 나오게 된다.
위의 함수는 목표치와 차이가 날 수밖에 없는데 이를 최소제곱법을 이용하여 차이(cost)를 구해보자.
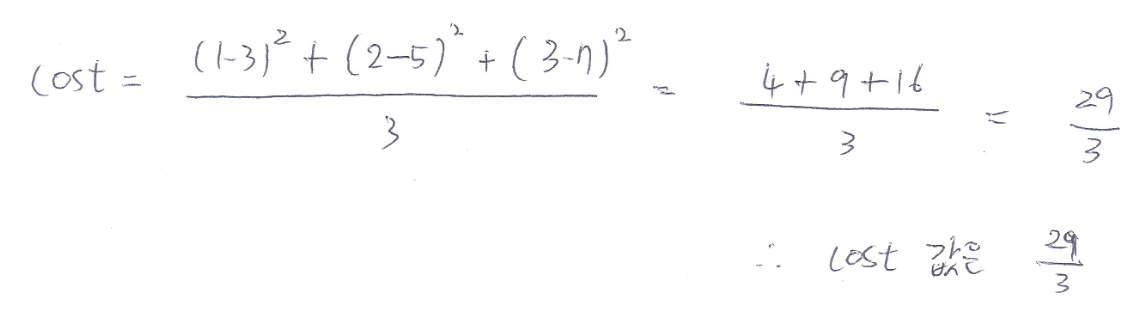
이를 통해 우리는 손실함수의 공식을 구할 수 있다.
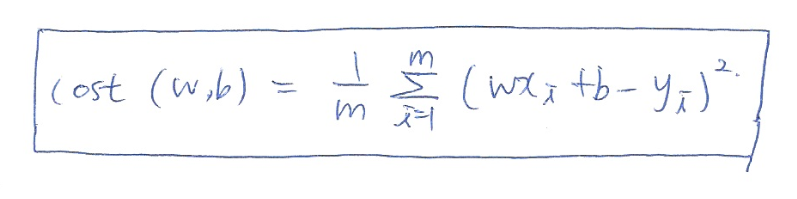
그런데 한가지 의문이 든다. 우리가 필요한 것은 목표치와의 차이인데 왜 제곱을 하는 것일까? 이는 두 가지의 이유가 있다.
① 차이를 제곱하여 그 패널티를 크게 하기 위해서
② 음수를 양수로 표현하여 연산을 편리하게 하기 위해서
▶ 문제를 해결하다, 경사 하강법
최소 제곱법을 이용한 손실함수를 통해 무엇이 문제이고, 얼마나 차이가 있는지를 파악하였으므로 이 차이를 줄여서 목표 값에 도달하여보자. 이 과정에는 경사하강법을 사용한다.
경사하강법에는 편미분이 사용이 된다. 편미분에 대하여 알아보자.
편미분의 사전적 정의는 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 생각하여 미분하는 것이다. 즉 미분하고자 하는 변수외에는 나머지 변수들을 상수 취급을 하는 것이다. 예를 들어보자.
다음과 같은 함수 f(x,y)가 있다고 하자.
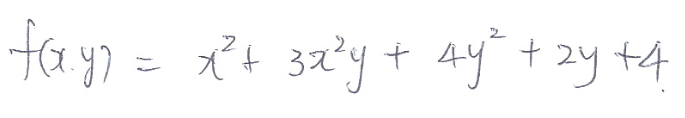
이 함수를 x에 대하여 편미분을 해보면 다음과 같다.
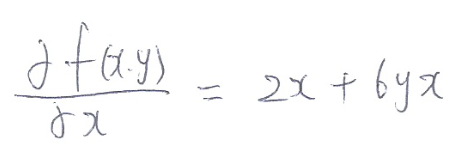
x를 제외한 y는 상수로 취급이 되어 미분이 되었다. y에 대한 편미분 역시 비슷하다.
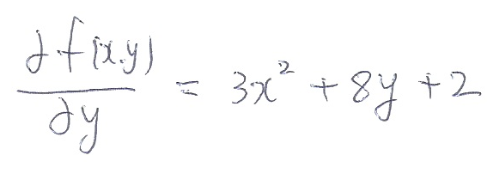
x가 상수로 취급이 되어 미분이 되었다. 이 정도의 개념만 숙지하면 경사하강법을 공부하는데는 충분하다.
다시 말하지만 우리의 목표는 적절한 w 값과 b값을 찾는 것이다. 위에서 편미분한 값을 w값에서 빼준다.

이 과정에서 학습률이라는 것이 사용이 되는데 학습률이 너무 작으면 학습속도가 느리고 학습률이 크다면 목표값을 지나칠 수 있기 때문에 적절한 크기의 학습률을 정하는 것이 매우 중요하다.

적절한 학습률을 정해준 뒤, 목표치에 접근하는 과정을 충분히 해준다면 우리가 원하는 값을 구할 수 있을 것이다.
'🖥️ 컴퓨터공학 🖥️ > 머신러닝, 딥러닝' 카테고리의 다른 글
| [ 딥러닝 알아가기 ] 경사하강법, 역전파, SoftMax 함수 (0) | 2020.12.24 |
|---|---|
| [ tensorflow ] 간단한 선형회귀모델 만들기 (0) | 2020.12.21 |
| [ Tensorflow ] tf.constant, tf.placeholder, tf.Variable의 차이를 알아보자 (0) | 2020.12.21 |
| [ Tensorflow 예제 ] Multi-variable linear Regression을 Tensorflow에서 구현 (0) | 2020.12.17 |
| [ Tensorflow 예제 ] Linear Regression의 cost최소화의 Tensorflow 구현 (0) | 2020.12.17 |