[ 딥러닝 알아가기 ] 경사하강법, 역전파, SoftMax 함수

▶ 손실함수와 경사하강법

 

 

 

머신러닝 모델은 위와 같은 구조로 이루어진다. 머신러닝모델에 입력값을 넣고, 출력값과 실제값의 차이를 구하여 이를 줄여가는 구조로 이루어져있다. 이때 출력값과 실제값의 차이를 손실, 비용, Cost라고 부르고, 이를 함수화한 것이 바로 비용함수이다. 그리고 비용함수의 함숫값을 줄여가는 방법으로 경사하강법이 이용된다. (Gradient Descent Algorithm)

 

비용함수와 경사하강법에 대하여 자세한 내용은 아래 링크에서 다루고 있다.

 

newindow.tistory.com/118?category=1137097

[ 딥러닝 알아가기 ] 선형회귀(Linear Regression)와 경사하강법

 

경사하강법은 손실 함수의 최소점을 찾는 알고리즘이며, 함수의 경사를 구하여 사용한다. 

경사하강법은 크게 3가지의 종류가 있다. 

 

1. 직관적인 경사 하강법

말 그래도 자신의 직관을 믿으면서 최소점을 찾아가는 방법. 이 글에서는 다루지 않는다.

 

2. 완전(배치)의 경사하강법

 

 

https://atcold.github.io/pytorch-Deep-Learning/ko/week02/02-3/

 

완전 배치 경사하강법은 최솟값을 구하는 가장 근본적인 알고리즘이지만 크게 2가지의 단점이 존재한다.

 

1. 학습 데이터가 많은 대규모 문제에서는 모든 데이터를 적용하여 가중치를 구해야 하는데 이는 많은 컴퓨팅 자원 소모량을 요구한다. 

2. 가중치의 초기 설정값에 따라 극솟값 함정에 빠지는 경우가 존재한다. 경사하강법의 목적은 비용함수의 최솟값을 구하는 것이다. 최솟값과 극솟값에서 모두 미분계수의 값이 0이기 때문에 충분히 극솟값에 수렴할 수 있다.

 

3. 확률적 경사 하강법 (Stohastic Gradient Descent, SGD)

배치 경사 하강법의 문제점을 해결하기 위해 도입된 방법이다. 이는 학습시간이 병목이 경우에 사용한다.  SGD는 배치 경사하강법과 달리 전체 학습 데이터 중 확률적으로 선택한 하나의 샘플을 사용한다. 이 때의 샘플은 학습데이터를 shuffle하여 임의로 선정하기 때문에 cost함수를 최소화하는 점으로 수렴하는 경로가 규칙적이지 않고 zig-zag모양을 보인다. 이를 통해 지역 최솟값, 극솟값에 빠지지 않고 탈출할 수 있다. 

하지만 최적의 학습률을 구하기 위해 사용자가 일일이 튜닝하는 작업이 필요하며, 수렴 조건을 그때그때 조정해야 한다.

 

4. 미니배치 경사하강법

배치 경사하강법과 SGD의 장점만을 취하여 만든 알고리즘. 이 글에서는 다루지 않는다.

 

▶ 역전파 알고리즘 (BackPropagation)

DNN(Deep Neural Network)는 은닉층을 지니고 있는 신경망으로, 중간에 sigmoid함수도 추가가 되면서 복잡한 구조를 띄게 되었다. 이러한 복잡한 구조 속에서 가중치를 구하고, 가중치 업데이트를 하기 위해선 어마어마한 계산량이 요구된다.

 

https://www.youtube.com/watch?v=573EZkzfnZ0&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm&index=27

 

 

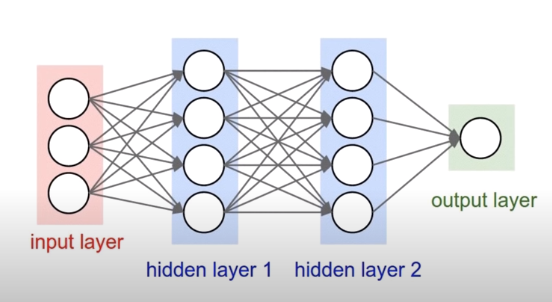
Minsky 교수는 1969년에 Perceptrons라는 논문을 통해 DNN은 불가능함을 설명하기도 하였다. 

 

 

https://www.youtube.com/watch?v=573EZkzfnZ0&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm&index=27

 

 

이 시기에 인공지능 침체기를 맞게 된다. 

그러다가 1980년대에 Paul Werbos, Hinton 교수가 고안한 역전파 개념으로 인해 다시 인공지능은 다시 붐을 맞이하게 된다. 

 

원래는 이 글에서 역전파를 다루려고 하였으나, 전체적인 내용을 보았을 때 스압 주의보가 내릴 것 같아 따로 글을 작성하였다. 역전파 알고리즘은 아래 링크에서 자세하게 다루었다.

 

newindow.tistory.com/218

[ 딥러닝 알아가기 ] 역전파(backpropagation) 제대로 이해하기

 

▶ SoftMax, LogSoftMax

Softmax란 무엇인가?

 

 

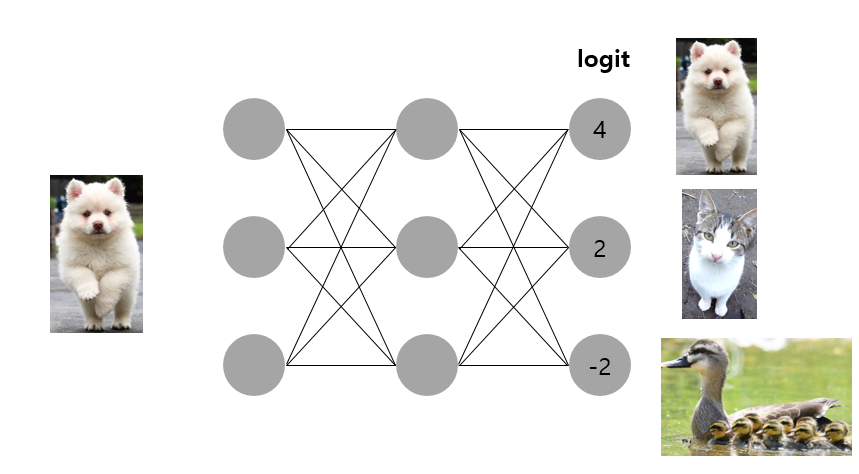
다음과 같은 모델이 있다고 하자. 이 모델을 보면 input 데이터로 들어온 강아지 사진을 모델을 통해 강아지임을 알게 되었다. 

 

https://www.slideshare.net/RickyPark3/2-68876167

 

이 때 우리는 logit이라는 개념을 이용하여 판단한다. logit 함수식은 ln(p/1-p)이며, p가 0%일 때는 -무한대, p가100%인 경우에는 +무한대이다. 

 

 

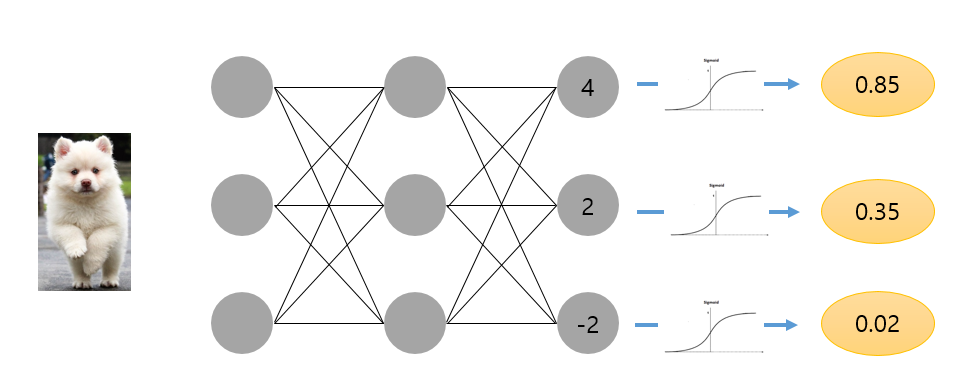
마지막 layer에 sigmoid 함수를 activation function으로 활용하여 적용한다면, 위의 그림과 같이 확률값을 알 수 있고, 강아지가 될 확률이 85%이므로, input 데이터는 강아지라는 결론을 도출할 수 있다. ( Binary Classification using Sigmoid)

하지만 이는 모든 클래스에 대한 확률이 아니라 각 클래스에 대한 확률이다. 우리는 이 확률값이 모든 클래스에 대하여 나오기를 원한다. 이 때 SoftMax 함수를 사용하여 나타낸다. (Mulit Classification using Softmax)

 

 

 

https://www.machinecurve.com/index.php/2020/01/08/how-does-the-softmax-activation-function-work/

 

 

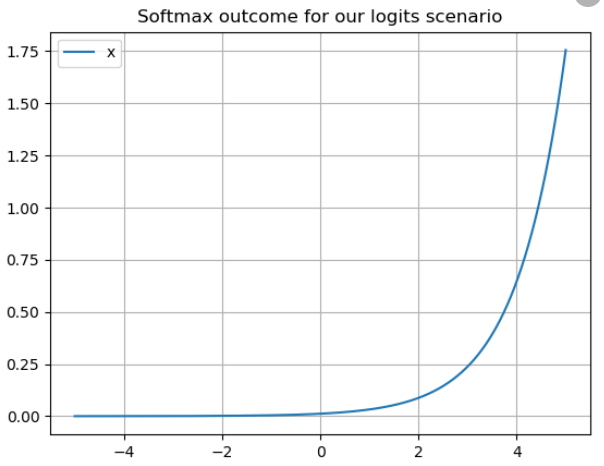
SoftMax함수의 함수식은 e^(logit) 이다. 위에서 찾은 logit값을 SoftMax로 나타내면 아래와 같이 나온다.

 

 

 

 

SoftMax함수는 모든 클래스에 대한 확률을 다루므로, 세 클래스에 대한 확률이 1이 되도록 만든다.

딥러닝모델을 학습할 경우, 다중 분류를 할 때 주로 one-hot encoding을 이용한다. 또한 확률값이 높은 값은 아주 높게 변환하고, 낮은 값은 아주 낮게 변환하는 cross-entopy를 통하여 학습할 수 있다.

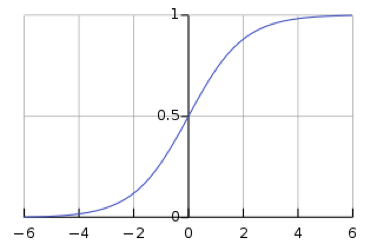
sigmoid함수에서 0.5를 기준으로 0.879는 1에 가깝고, 0.119와 0.002는 0에 가까우므로 [1,0,0] 벡터로 변환이 될 수 있음을 알 수 있다. 

Softmax함수의 보완형, LogSoftmax

그러나 SoftMax 함수를 사용하면 기울기 손실(Vanishing Gradients)이 발생하여 신경망의 가중치가 학습되는 것을 막는다. 활성화 함수 중 하나인 Sigmoid함수는 logit함수의 역함수로, 이를 일반화시키면 SoftMax함수가 된다. 이 때 Sigmoid함수 h(s)는 s값이 매우 커서 1인 경우나 매우 작아 0인 경우에 평평해지기 때문에 기울기가 0이 되어 손실이 발생하게 된다. 

 

 

 

 

LogSoftMax 함수는 SoftMax 함수에 로그를 취한 함수이다.

 

 

 

 

위의 식을 정리하면 logsoftmax함수는 아래와 같이 정리할 수 있다. 

 

 

 

 

 

s가 매우 작은 경우에는 0이고, s가 매우 큰 경우 값은 s이다. 결과적으로 결과값이 포화되지 않고 기울기 손실 문제를 피할 수 있다.

 

 

 

 

▶ 인공신경망

newindow.tistory.com/221?category=1171494

[ PyTorch ] Pytorch로 나선형 분류하기 예제