걸린 시간 : 49분
난이도 : 중
문제1
기하와 벡터이므로 제외
문제 2-1



잘한 점
=> 가운데 식이 적분의 형태이므로 이를 힌트로 하여 푼 점이 잘하였다. 우선 sinb-sinx함수를 그래프로 그린 후, 양 옆의 함수를 적분한 형태인 y = cosb(b-x)와 y = cosa(b-x)를 그린다.
세 함수 모두 (b,0)을 지난다. [0,π] 구간에서 y = cosx는 감소함수이고, a<b이므로 cosa>cosb, -cosa<-cosb이다.
그리고 a를 대입하였을 때 cosa(b-x)가 가장 작고, 그 다음으로 sinb-sina, 그리고 cosb(b-x)가 가장 커야 한다.
이는 평균값 정리를 이용하여 해결하였다.
피드백
=> 답지 풀이를 보니 처음부터 평균값 정리를 사용하였다. a<x<b이 실수 x에 대하여
sinb-sina = (b-a)cosα를 만족하는 α값이 구간 (a,b) 내에 존재한다. ------- (ㄱ)
f(x) = sinx라 할 때, [0,π]에서 f'(x)는 감소함수이므로,
cosa > cosα > cosb이다.
(b-x)>0이므로
(b-x)cosa > (b-x)cosα > (b-x)cosb 가 성립한다.
(ㄱ)에 의하여 (b-x)cosα = sinb - sinx이다.
따라서 위의 부등식은 성립한다.
나의 풀이는 일관성이 없었지만 답지 풀이는 일관성도 있으면서 더 쉬운 듯하다.
문제 2-2


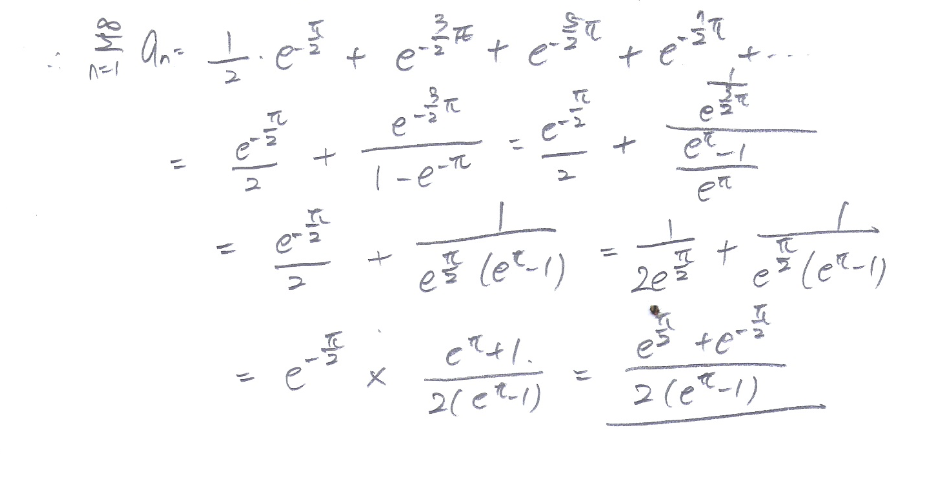
잘한 점
=> 꽤 복잡한 계산이었는데도 잘 하였다. 또한 부호도 잘 신경써서 잘 하였다.
피드백
=> 피드백은 딱히 없는듯 하다.
문제 2-3

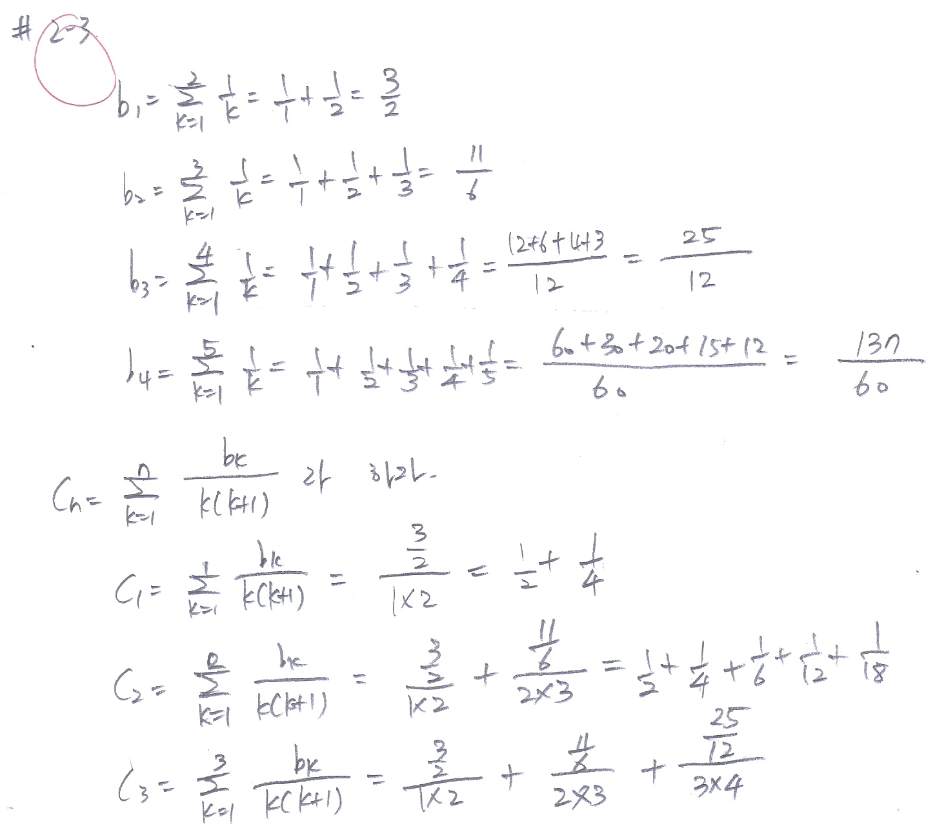


잘한 점
=> 근 내가 푼 수학문제들 중 가장 뿌듯한 문제이다. 수열의 규칙성을 찾을 때 괄호를 치면서 풀어나간 것이 많은 도움이 되었다. 애용하자
피드백
=> 이것 역시 딱히 필요가 없는 듯 하다.
'🔍 정보 공유 🔍 > 대입 논술 입시자료 정보' 카테고리의 다른 글
| [연세대] 2020 자연계열 수리논술 오전 (0) | 2020.09.30 |
|---|---|
| [한양대] 2018 자연계열 오전 (0) | 2020.09.29 |
| [한양대] 2020 자연계열 오후2 (0) | 2020.09.15 |
| [한양대] 2020 자연계열 모의논술 1차 (0) | 2020.09.15 |
| [한양대] 2018 자연계열 오후1 (0) | 2020.09.15 |