걸린시간 : 미측정
난이도 : 上
문제 1



잘한 점
=> 치환적분을 적용하여 접근하였다. 하지만 중간에 치환하는 과정에서 약간의 꺼림직함이 있다.
피드백
=> 답지는 f<n-1>을 치환하여 계산하였다. f<n-1>을 미분하면 분자와 분모가 계속해서 약분이 되어 분자는 다 1이 남게 되고, 분모는 f<n-2>부터 f<0>까지 곱한 값이 남게 된다. 이를 이용하여 치환적분을 하였다.
문제 2



잘한 점
=> 쉽지 않았던 문제이다. 하지만 원 문제가 나온다면 가장 중요한 것은 중심과 반지름이라는 점을 잊지 말아야 한다. 또한 접선이 나온다면 접점과 중심을 잇는 것은 정말 중요한 단서가 된다는 점도 잊지 말아야 한다. 다행히 이 점을 기억해내어서 문제를 풀 수 있었으나 마지막에 a를 θ로 표현하지 않았다.
피드백
=> 위에서 언급했던 대로, 원 문제가 나온다면 가장 중요한 것은 중심과 반지름이라는 점과, 접선이 나온다면 접점과 중심을 잇는 것은 정말 중요한 단서가 된다는 점을 이용하는 문제이다. 이 점이 제일 중요하지 않았나 싶다.
문제 3

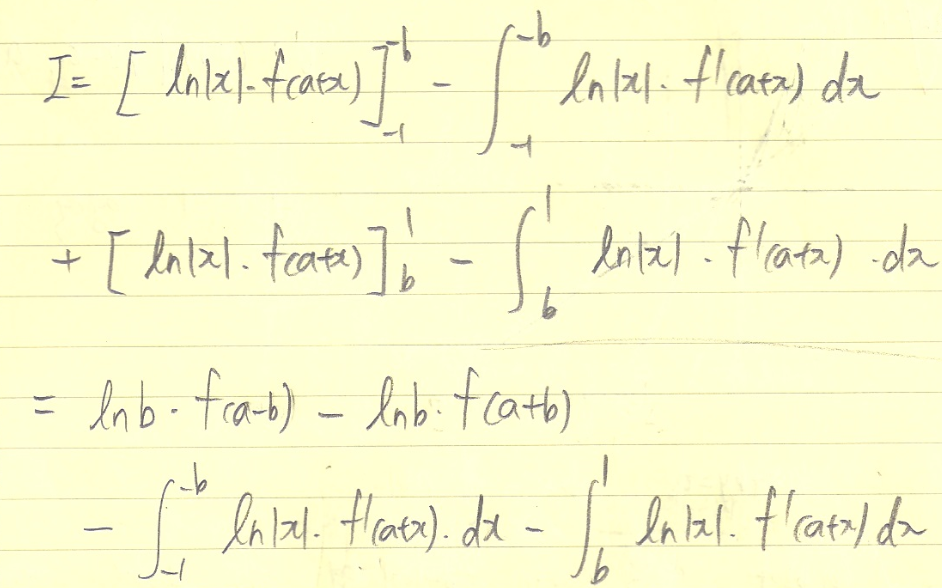

잘한 점
=> 없다. 문제에서 말하고자 하는 포인트조차 잡지 못하였다. 적분이 나오면 크게 3가지 방법이 있다. 첫 번째, 그냥 적분을 한다. 두 번째, 치환 적분을 한다. 세 번째, 부분 적분을 한다.
Integral 안에 있는 함수를 보니 첫 번째 방법은 f(a+x)를 모르기 때문에 불가능하고, 두 번째 방법인 치환적분을 해도 소용이 없을 것 같아 부분적분을 이용하였다.
중간에 평균값 정리도 떠올리긴 했다. 그런데 부분적분을 한 결과에 평균값 정리를 적용하려 하였으므로 소용없었다.
피드백
=> 평균값 정리를 이용하는 문제이다.
우선 치환적분을 하여 저 두 식을 하나의 Integral 안에 넣어준다. 각각의 항의 있는 함수가 같기 때문에 떠올릴 수 있는 아이디어인듯 하다.
이렇게 합친 함수를 이용하여 평균값정리를 적용한다. [a-x,a+x]에 평균값정리를 만족하는 상수 c가 있음을 찾았다. 그런데 도함수 f'(x)는 모든 실수 x에 대하여 |f'(x)| <=1이라고 했으므로
-2 <= (f(a+x)-f(a-x))/2x <= 2를 만족한다.
Integral을 씌우고 0<b<1이라는 조건을 이용하여 적분을 하면 제시문의 질문을 증명할 수 있다.
문제 4



잘한 점
=> 어려운 문제는 아니지만 중간에 ax + by >=0의 (a,b)가 영역 C에 포함되는지 파악하는 부분이 많이 헷가린다. (사실 지금도 잘 모르겠다. 인터넷을 찾아봤는데 해설이 나오지 않는다...!)

잘한 점
=> 문제 4-1에서 얻은 결과를 이용하기만 하면 되는 문제이다. 그다지 어렵지 않았다.
피드백
=> 문제 4-1의 결과를 이용하고, 각각의 부채꼴의 중심각을 구할 수 있는지 물어보는 문제이다.

잘한 점
=> 문제 4-1 처럼 풀면 된다. 딱히 어렵지는 않았다.
'🔍 정보 공유 🔍 > 대입 논술 입시자료 정보' 카테고리의 다른 글
| [공대생이 푸는 모의고사] 2021년도 9평 지구과학1 풀이 (2 ~ 8) (0) | 2020.10.01 |
|---|---|
| [한양대] 2017 자연계열 오전 (0) | 2020.09.30 |
| [연세대] 2020 자연계열 수리논술 오전 (0) | 2020.09.30 |
| [한양대] 2018 자연계열 오전 (0) | 2020.09.29 |
| [한양대] 2018 자연계열 오후2 (0) | 2020.09.29 |