난이도 : 상(특히 2-2번과 3-3.)
문제 제시문 + 1번


잘한 점
=> 이 문제는 a+2b+c=4를 a+b+b+c로 분리를 하는 것이 포인트이다. 이 점을 캐치하여 잘 풀었다.
피드백
=> 답지에서는 코시 - 슈바르츠 방정식을 이용하여 풀었다.
문제 2 제시문

문제 2-1



잘한 점
=>식1 과 식2를 보면 식2를 푸는데 식1이 사용됨을 알 수 있다. 따라서 이 문제를 풀기 위해서는 차례대로 규칙을 잡아야 한다. 이 점을 잡고 풀이과정을 세웠다.
피드백
=> 우선, 제시문을 보니 X, Y, Z 모두 깔끔하게 정리가 되어있어서 답도 깔끔하게 나와야 하는 줄 알았다. 하지만 막상 풀어보니 너무 더럽게 나오고 복잡하여 풀다가 그만두었다. plus, 너무 많이 풀이과정을 차지하는 것 같았다. 하지만 답지 풀이를 보니 내가 푼 방법이 맞았다.
가끔 풀 때 어 이게 맞는가? 라는 생각이 들 때가 있는데, 그때마다 이 문제를 떠올려야 겠다. 내가 지금까지 풀어본 문제르 훑어 보고, 풀이 접근 방식이나 풀이과정에서 하자가 없다면 그대로 밀고 나가는 것이 맞는듯 하다.
문제 2-2
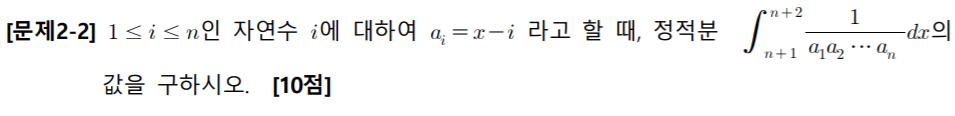
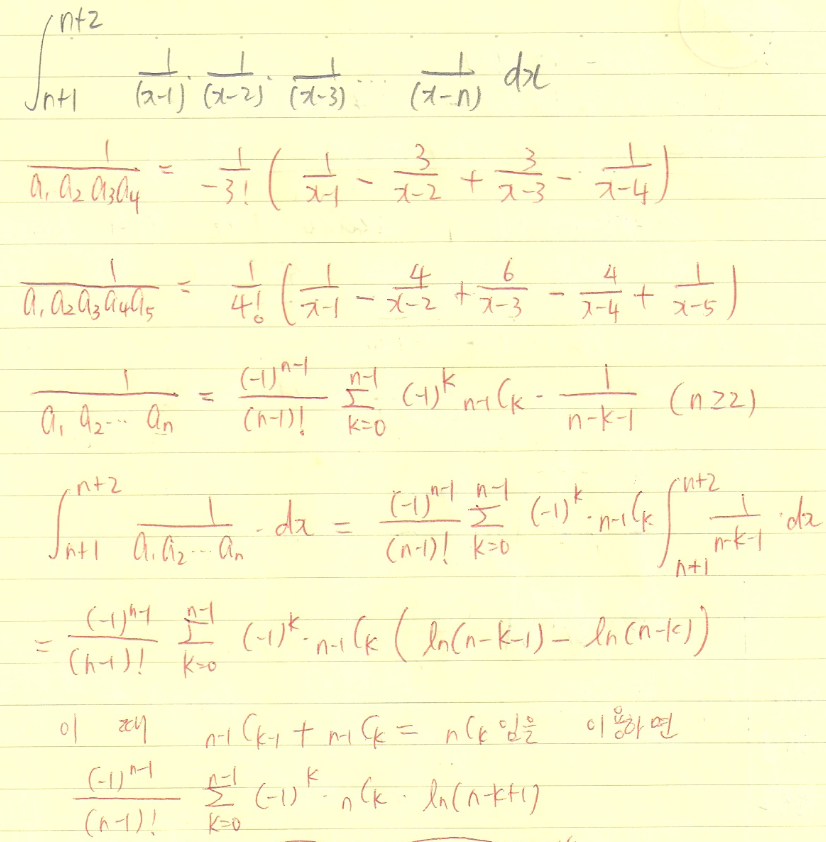
잘한 점
=> 없다. [문제 2-1]에서 나온 결과로만 풀 수 있는 문제인 줄 알았고, 분수의 합차꼴로 만든다는 생각을 하지 못하였기 때문에 접근을 하지 못하였다.
피드백
=> 먼저 [문제 2-1] 처럼 분수들의 합차 형태로 나타내야 한다. 그리고 이를 n에 대해서 일반화를 시킨다. 이 과정에서 수학적 귀납법이 사용된다.

이제 이 식을 n+1 부터 n+2 까지 x에 대하여 부분적분을 시킨다.
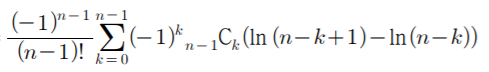
다음과 같이 결과가 나온다. 이제 ln(n-k+1)과 ln(n-k)를 분리한 뒤 이항정리를 통해 간단하게 만들어준다.
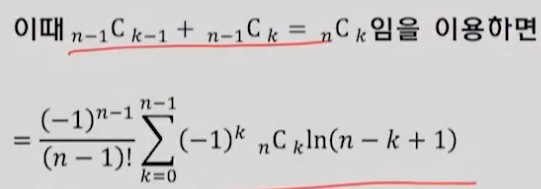
정리하자면
먼저 분수의 합차꼴로 변형을 시킨다.
수학적 귀납법을 통해 n개의 분수가 있을 때를 일반화한 식을 구한다.
이 식을 x에 대하여 부분적분한다.
이항정리를 이용하여 식을 간단하게 만든다.
문제 제시문 + 3-1


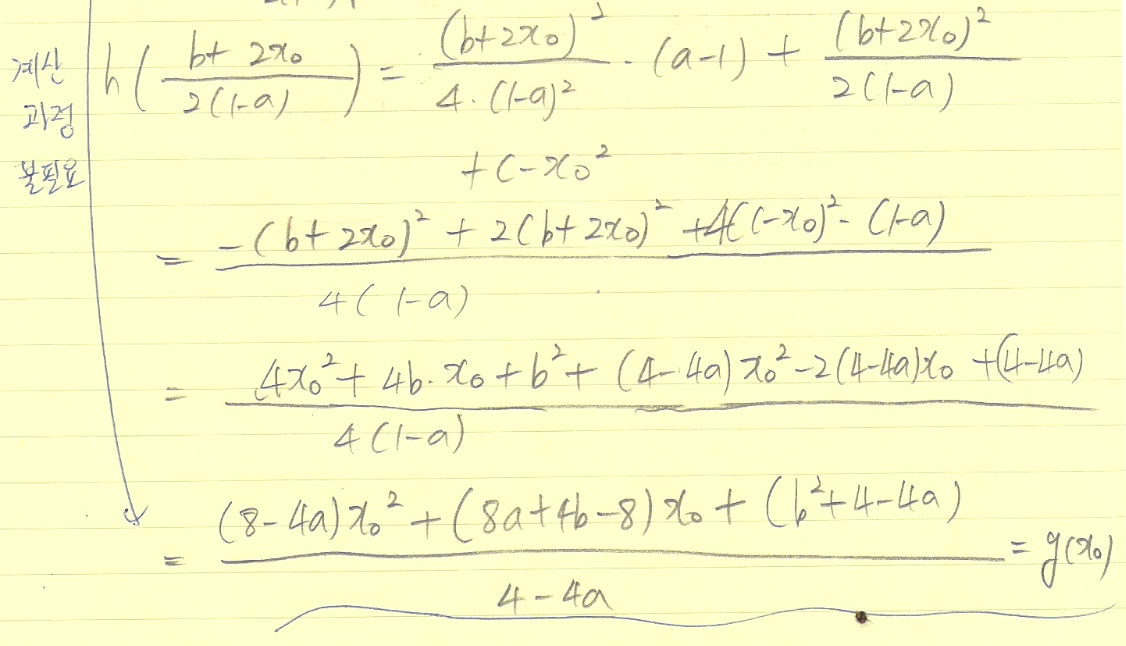
잘한 점
=> 잘 풀었다. (x-x0)^2를 뺀 함수를 미분한 뒤, 이 함수가 위로 볼록이기 때문에 꼭짓점 지점에서 최댓값 g(x0)를 가진다는 점을 잘 서술하였다.
피드백
=> 다만 어려운 문제가 아닌데도 쓸데없는 말을 많이 넣어 길게 쓴 느낌이 든다. 하지만 너무 간단하게 써서 중요한 부분을 놓치는 것보다는 길게 써서 감점을 받지 않는 것이 훨씬 더 좋다.
문제 3-2


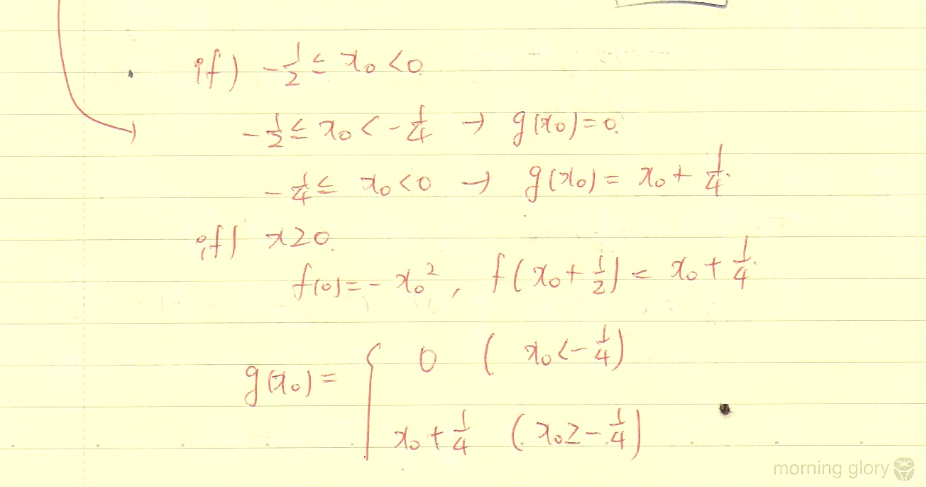
잘한 점
=> x0의 범위를 나누어서 각 범위에 있을 때의 최댓값을 구하는 것이 이 문제의 포인트이다. 이 점을 잘 캐치하였다.
피드백
=> 계산실수를 하였다. 문제를 옮길 적에 잘못 옮겼다. 아래 문제도 비슷한 맥락인데, 이 문제는 시간을 착각하여 막판에 너무 급하게 풀어서 실수가 발생하였다. 하나하나 범위를 따지면서 들어갔으면 틀리지 않았을 문제.
문제 3-3

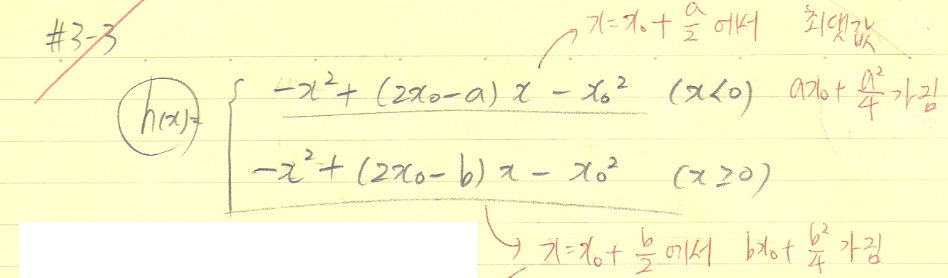
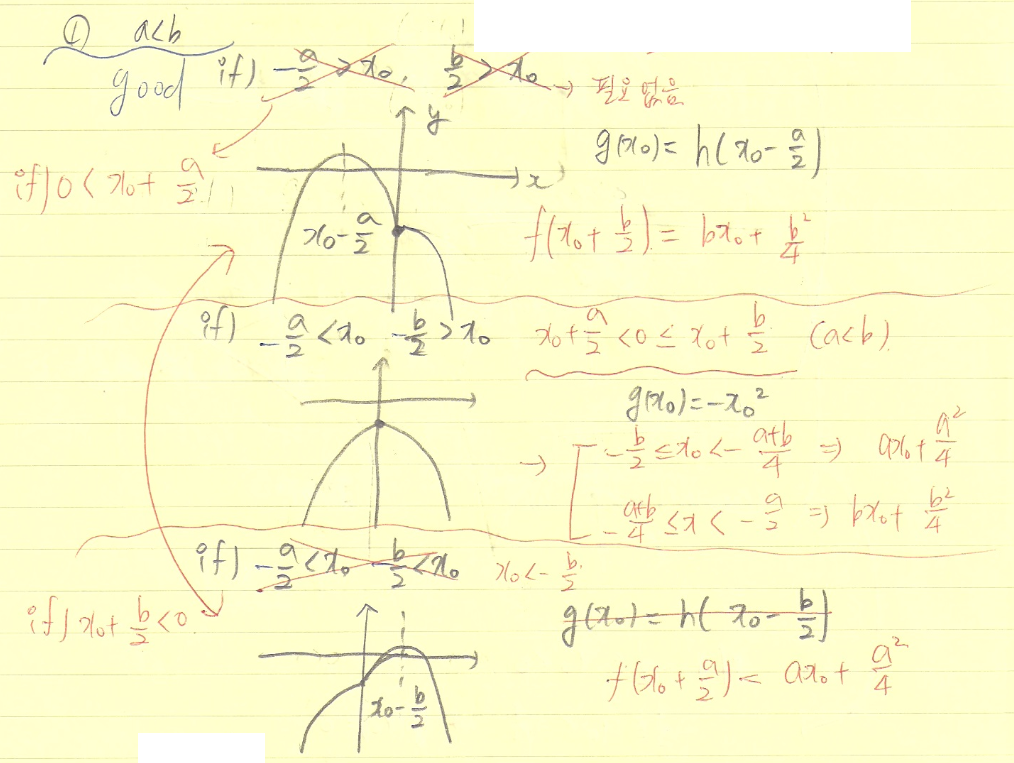
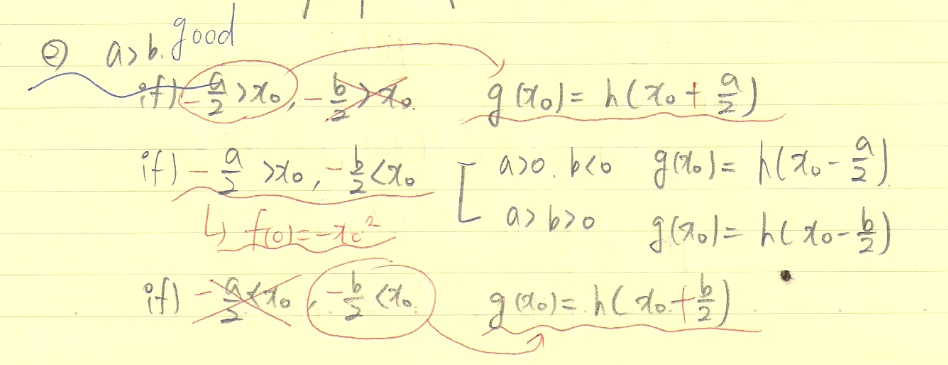
잘한 점
=> 우선 보자마자 a와 b의 범위를 구해야 함을 알아야 한다. 또한 위의 문제처럼 x0의 범위도 따져야 한다. 시도는 좋았으나 너무 대충푼 느낌이 들어 아쉽다.
피드백
=> 그림 그리는 것 okay. 아주 좋았다. 하지만 범위를 설정하는 과정에서 실수가 발생하였다. 헷갈릴 때는 나의 풀이를 객관화하면서 하나하나 차분히 따져보자.
문제 3-4


잘한 점
=> Nope
피드백
=> [문제3-3]을 풀었다면 풀 수 있었을 문제. 각 조건에 따른 함수가 연속인지를 판단하는 문제
'🔍 정보 공유 🔍 > 대입 논술 입시자료 정보' 카테고리의 다른 글
| [한양대] 2017 자연계열 오후1 (0) | 2020.10.17 |
|---|---|
| [연세대] 2021 자연계열 지구과학 모의논술 (0) | 2020.10.15 |
| [공대생이 푸는 모의고사] 2021년도 9평 지구과학1 풀이 (2 ~ 8) (0) | 2020.10.01 |
| [한양대] 2017 자연계열 오전 (0) | 2020.09.30 |
| [연세대] 2020 자연계열 수리논술 오후 (0) | 2020.09.30 |

