난이도 : 상
걸린 시간 : 44분 23초
문제 1 제시문

문제 1-1


잘한 점
=> 위에서 주어진 숫자를 대입해서 값을 구하기만 하면 되는 문제. 너무 쉬웠다.
피드백
=> 없음.
문제 1-2
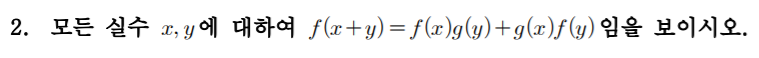

잘한 점
=> 정말 못풀었던 문제. 주어진 조건을 가지고 생각을 해봐야 하는데 말이다...
피드백
=> 현재 우리는 f(0) = 0, f(8) =1 , g(0) = 1, g(8) = 0을 알고 있다. 그러면 이 조건을 이용해서 한번 풀어봐야 한다.
제시문에는 다음의 조건이 있다.
g(x-y) = g(x)g(y) + f(x)f(y)
여기에 x=8, y=x를 대입한다.
g(8-x) = g(8)g(x) + f(8)f(x) = f(x) --------------(ㄱ)
x = 8-x 대입
g(8-(8-x)) = g(x) = f(8-x) ----------(ㄴ)
[문제 2-2]에 나온 식은 다음과 같다.
f(x+y) = f(x)g(y) + g(x)f(y) = g(8-(x+y))
g(8-x-y) = g(8-x)g(y) + f(8-x)f(y) = f(x)g(y) + g(x)f(y) (∵ (ㄱ), (ㄴ))
따라서 성립!
=> 이 문제에서 g(8-x) = f(x)임을 발견하고, f(x+y)에 8과 y를 대입하는 것이 포인트이다.
문제 1-3



잘한 점
=> 문제를 너무 못풀겠어서 함수를 지정하고 풀었다. 실전에서 이러면 0점!!!!
피드백
=> 미분가능하다는 조건을 주고, 도함수값을 주었다. 이럴 때는 일반적으로 미분가능하기 때문에 f(x)를 미분을 할 것이다. 하지만 f(x) 함수의 식을 모르기 때문에 이럴 때는 순간 변화율의 모델을 가져와서 접근한다.
=> 정리를 하자면, 문제에서 미분가능하다는 조건을 주고, 도함수 값을 준다면 원함수를 미분하여 식의 형태를 관찰하던가, 아니면 이 문제처럼 순간변화율의 모델을 가져와서 접근한다
문제 2 제시문

문제 2-1



잘한 점
=> 원래 나의 풀이 방향은 부등호를 중심으로 좌우의 함수 그래프를 그린 뒤, 대소 비교를 하려고 했다. 근데 오른쪽에 있는 그래프를 잘 그리지 못하였다.
=> 가장 어려웠던 부분은 x = -1+√3 에서 f(-1+√3)과 g(-1+√3)의 대소비교가 어려웠다.
이 부분은 바로 g''(x)를 구함으로서 해결할 수 있다. g''(x)는 x = 0, -4에서 변곡점을 갖기 때문에 f(x)와 g(x)의 유일한 교점인 (0,1)에서 함수 g(x)가 위로 볼록해지는 것을 알 수 있다. 더 나아가 함수 f(x)가 g(x)의 x=0에서 변곡접선이라는 사실을 알 수 있다.
=> 그래프가 잘 안그려지만 이계도함수까지 그려보자
피드백
=> 위에서 말한 방식대로 그래프만 잘 그리면 t>0에서의 대소비교는 쉬울 것이다.
문제 2-2


잘한 점
=> 없음.
피드백
=> P(0)>0이라는 것은 매우 쉽게 구할 수 있다.
=> P(-2n)이 문제이다. 우선 수열에서 가장 일반적인 접근 방식인 n=1부터 대입하는 방식대로 해보자. 대입을 하고 모든 자연수 k에 대하여 2k-1번째의 항과 2k번째 항을 묶는다. 그리고 이 두 항을 더한 값이 0보다 작다는 것을 증명함으로서 P(-2n) <0임을 보여주면 풀 수 있다.
=> 2k-1번째 항과 2k번째 항을 묶는 발상이 조금 어려운 듯하다. 아래 링크의 2-3번 문제도 항을 묶어서 푸는 접근 방식이다.
[한양대] 2018 자연계열 오후2
걸린 시간 : 49분 난이도 : 중 문제1 기하와 벡터이므로 제외 문제 2-1 잘한 점 => 가운데 식이 적분의 형태이므로 이를 힌트로 하여 푼 점이 잘하였다. 우선 sinb-sinx함수를 그래프로 그린 후, 양 옆��
newindow.tistory.com
문제 2-3



잘한 점
=> P'(2n) = P(2n-1)을 발견하였다.
피드백
=> 우선 x=0을 중심으로 양수일 때와 음수일 때로 나눈다. 양수일 때는 무조건 0보다 크기 때문에 실근을 갖지 않는다.
=> P'(2n) = P(2n-1)을 이용한다.
수학적 귀납법을 통해 P(2n-2)이 항상 0보다 크다고 가정한 뒤, P(2n-1)이 증가함수임을 찾아낸다. 그리고 P(2n-1) = 0을 만족하는 t값이 [문제 2-2]을 통해 -2k < t< 0임을 찾고, 함수 P(2n)가 x=t에서 극솟값(최솟값)을 가짐을 증명한다. 함수 P(2n)의 극솟값이 0보다 크기 때문에 실근을 갖지 않는다.
'🔍 정보 공유 🔍 > 대입 논술 입시자료 정보' 카테고리의 다른 글
| [한양대] 2017 자연계열 오후 2 (0) | 2020.12.04 |
|---|---|
| [한양대] 2019 모의논술 자연계열 1차 (0) | 2020.11.18 |
| [연세대] 2021 자연계열 지구과학 모의논술 (0) | 2020.10.15 |
| [연세대] 2021 자연계열 수리논술 모의논술 (0) | 2020.10.15 |
| [공대생이 푸는 모의고사] 2021년도 9평 지구과학1 풀이 (2 ~ 8) (0) | 2020.10.01 |