[경제성공학] 이자율이 실시간으로 계속 변하는 경우

이자율이 아래 그림과 같이 실시간으로 변한다고 가정하자. 

 

http://irvinehomesource.com/부동산-계약서/모기지-이자율-사상-최저에서-2주연속-오름세3-19일-현/

 

현재는 t = 0이고, $r(s)$는 시간 s시기에서의 이자율이다.

 

만약 s시기에 $x$라는 금액을 은행에 투자하였다면, h만큼 지나고 s+h시기에 은행에 쌓이는 금액은

$$x(1+r(s)h)$$

라고 할 수 있다.

 

※ 연간이자율과 월복리

예를 들어 연간 이자율이 r라고 하고, 월 복리로 이자가 측정이 된다고 하면 한 달이 지나고 난 뒤에는 원금의 $\frac{r}{12}$배 크기의 이자가 쌓인다.

따라서 연간이자율$r$은 그 순간의 이자율인 $i$에 기간인 12를 곱한 $12i$가 된다.

 

위의 예시도 이와 같은 원리이다. s시기의 순간 이자율을 $r(s)$라고 했을 때, 그 값에 기간인 $h$를 곱한 $r(s)h$배 만큼의 이자가 쌓이므로 $x(1+r(s)h)$와 같은 결과가 나온다.

 

 

이렇게 이자율이 실시간으로 변화하는 상황(Continous Compounding)에서는 [현재에 돈을 넣고], [s시기에 돈을 뺐다가 다시 넣고], [s시기에 넣은 돈을 s+h시기에 돈을 뺐다가 다시 넣고] 이러한 과정을 t시기가 될 때까지 계속해서 반복한다. 

 

D(t) 구하기

---

 

$D(t)$ : 시기0일 때 은행에 1달러를 예금하고 t 시기에 받는 금액

$r(s)$ : s시기에서의 순간이자율

D(t)는 은행에 지금 현재 1달러를 예금했을 때 t시기에 받을 수 있는 금액!

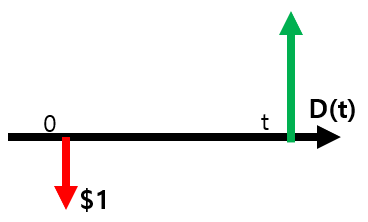
이를 바탕으로 $D(t)$를 일반화하여 표현해보도록 하겠다.

 

s시기에 쌓인 돈을 재빠르게 뺐다가 다시 은행에 넣는다.

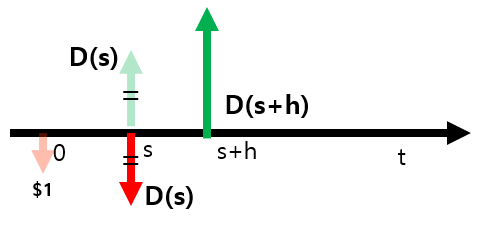
$D(s+h)=D(s)(1+r(s)h)$ (∵ $x(1+r(s)h)$)

 

$D(s+h) - D(s) = D(s)r(s)h$

 

$\frac{D(s+h) - D(s)}{h} = D(s)r(s)$

 

$\lim_{h \to 0} \frac{D(s+h) - D(s)}{h} = D'(s) = D(s)r(s)$

 

$D(s)$는 금액이므로 양수이므로 나눌 수 있다. $D(s)$로 양변을 나눈다.

 

$\frac{D'(s)}{D(s)} = r(s)$

 

각 항을 적분한다. 여기서 적분 변수 s의 범위는 0에서 t까지이다.

 

$\int_{0}^{t} \frac{D'(s)}{D(s)} \, ds$ = $\int_{0}^{t} r(s) \, ds$

 

$ \ln{D(t)} - \ln{D(0)} = \int_{0}^{t}r(s) \, ds$

 

$D(0)$은 1이므로 $\ln{D(0)} = 0$

 

따라서

 

$\ln{D(t)} = \int_{0}^{t}r(s) \, ds$ 이므로

 

$D(t)$는 $e^{\int_{0}^{t} r(s) \, ds}$로 나타낼 수 있다.

 

 

P(t) 구하기

---

 

$P(t)$ : t시기에 회수하는 금액이 1달러가 되게 하도록 하는 현재 시기 투자 금액

P(t)는 t시기에 금액을 회수했을 때 1달러가 되게 하도록 하는 현재 시기에 투자하는 금액!!

 

비례식을 통해 $P(t)$를 $D(t)$를 이용한 식으로 나타낼 수 있다.

 

$$P(t) : 1 = 1 : D(t)$$

 

따라서 $P(t)$는 $\frac{1}{D(t)} = e^{-\int_{0}^{t} r(s) \, ds}$이다

 

 

 

$\bar{r}(x)$를 0기부터 t기까지 실시간으로 변하는 이자율들의 평균 값(평균 이자율)이라고 가정하자. 그러면 아래의 식이 만족하게 된다.

 

$$e^{\int_{0}^{t} r(s) \, ds} = t\ \bar{r}(x)$$

 

$P(t) = e^{-\int_{0}^{t} r(s) \, ds}$이므로 $P(t)$는 $e^{-t \bar{r}(x)}$라는 결론을 얻을 수 있다