목적 : LogNormal Distribution 관점에서 GBM의 평균과 표준편차를 구한다.
1. t기 후의 최종 주식 가격을 일반화시킨다.
현재 시기를 0이라고 하고, t기 후의 최종 주식 가격을 일반화시켜본다.
1) 우선 t를 n으로 나누어 단위 시간이 될 $\Delta$를 $\frac{t}{n}$으로 정의한다.
주식 가격은 $\Delta$가 지날 때마다 오르고 내리고를 n번 반복한다.
2) 확률변수 $Y_i$를 다음과 같이 정의하자 (베르누이 확률분포)
$Y_i$ = 1 (주식 가격이 상승할 때), 0 (주식가격이 하락할 때)
$Y_0$부터 $Y_n$의 값들을 전부 더하게 되면 주식가격이 하락한 경우는 값이 0이기 때문에 주식 가격이 상승한 경우만 반영이 된다.
위의 정의에 따라
$\Sigma Y_i$ : t시간 동안 주식 가격이 오른 횟수
$\Sigma (n-Y_i)$ : t시간 동안 주식 가격이 내린 횟수
로 상승횟수와 하강 횟수를 표현할 수 있다.
※ 주식 가격이 순서에 상관없이 상승(하강)한 최종 횟수가 같다면 최종 주식 가격은 동일하다.
ex) u = 1.05%, d = 0.9%, 초기 주식 가격 S(0) = 100 이라고 가정하자. 3년 뒤의 최종 주식 가격은?
- S(3) = S(0) x u x d x u = 100(1.05)(0.9)(1.05) = 108.9
- S(3) = S(0) x u x u x d = 100(1.05)(1.05)(0.9) = 108.9
정리하면 오르는 순서에 상관없이 최종 주식 가격은 $S(3) = S(0) u^2 d^1$ = 108.9이다.
3) 이제 t기의 최종 주식 가격을 일반화시켜본다.
$\Sigma Y_i$가 t시간 동안 주식 가격이 오른 횟수이고, $n - \Sigma (Y_i)$가 t시간 동안 주식 가격이 내린 횟수다.
따라서 최종 주식 가격 $S(t)$는
$S(t)$ = $S(0) u^{\Sigma Y_i} d^{\Sigma (n-Y_i)}$ = $S(0) d^n (\frac{u}{d})^{\Sigma Y_i}$로 나타낼 수 있다.
2. $\frac{S(t)}{S(0)}$가 lognormal 분포임을 고려하여 $\frac{S(t)}{S(0)}$의 평균 값 구하기
위에서 최종 주식 가격 $S(t)$는
$S(t) = S(n \Delta)$ = $S(0) d^n (\frac{u}{d})^{\Sigma Y_i}$ (∵ $t = \frac{n}{\Delta}$)
로 나타낼 수 있었다.
1) $S(t)$ 확률 변수를 시간에 따른 비율값으로 변형을 시켜준다.
$\frac{S(t)}{S(0)}$ = $d^n (\frac{u}{d})^{\Sigma Y_i}$
2) 각 항에 log를 취해준다.
$\frac{S(t)}{S(0)}$ = $d^n (\frac{u}{d})^{\Sigma Y_i}$
$log{ \frac{S(t)}{S(0)}}$ = $n \log{d} + \Sigma {Y_i} \frac{u}{d}$
3) $log{\frac{S(n\Delta)}{S(0)}}$의 기댓값(평균)을 구한다.
$log \frac{S(t)}{S(0)}$ = $n \log{d} + \Sigma {Y_i} \frac{u}{d}$
= $\frac{t}{\Delta} log{d}$ + $2\sigma \sqrt{\Delta}$ $\Sigma Y_i$
($n$ =$\frac{n}{\Delta}$, $u$ = $e^{\sigma \sqrt{\Delta}}$, $d$ = $e^{-\sigma \sqrt{\Delta}}$이므로)
$\frac{t}{\Delta} log d$ = $b$, $2 \sigma \sqrt{\Delta}$ = $a$, $\Sigma{Y_i}$ = $E(Y)$ 라고 하면
$E [log \frac{S(t)}{S(0)}]$
= E[$\frac{t}{\Delta} log d$ + $2\sigma \sqrt{\Delta}$ $\Sigma Y_i$]
= $\frac{t}{\Delta} log d$+ $2\sigma \sqrt{\Delta}$ E[$\Sigma Y_i$]
이때 E[$\Sigma Y_i$] = $p$이므로,
E[$log{\frac{S(t)}{S(0)}}$] = $2\sigma \sqrt{\Delta}$ $p$ $\frac{t}{\Delta}$ - $\frac{t\sigma}{\sqrt{\Delta}}$
$p = \frac{1}{2}(1 + \frac{\mu}{\sigma}\sqrt{\Delta})$ 이므로
$E [log \frac{S(t)}{S(0)}]$ = $t\mu$
3. $\frac{S(t)}{S(0)}$의 분산 구하기
$Var(log \frac{S(t)}{S(0)})$ = $Var$($2\sigma \sqrt{\Delta} \Sigma Y_i - \frac{t\sigma}{\sqrt{\Delta}}$)
이때 E[$\Sigma Y_i$] = $p$이므로,
= $(2\sigma\sqrt{\Delta})^2$ $Var(Y)$ = $4 \sigma^2 \Delta$ $p(1-p)$ $\frac{t}{\Delta}$
$Var(Y)$는 이항분포에 따라 $p(1-p)$이며, $\Delta$가 0으로 수렴하게 되면 원래 $\frac{1}{2}(1+\frac{\mu}{\sigma}\sqrt{\Delta})$였던 $p$는 $\frac{1}{2}$로 수렴한다는 점을 통해
$Var(log\frac{S(t)}{S(0)})$= $t\sigma^2$임을 알 수 있다.
4. 결론
확률변수 $\frac{S(t)}{S(0)}$는 로그정규분포를 따르고, $log \frac{S(t)}{S(0)}$ 은 정규분포 $N(t\mu, t\sigma^2)$를 따른다.
+ Summation




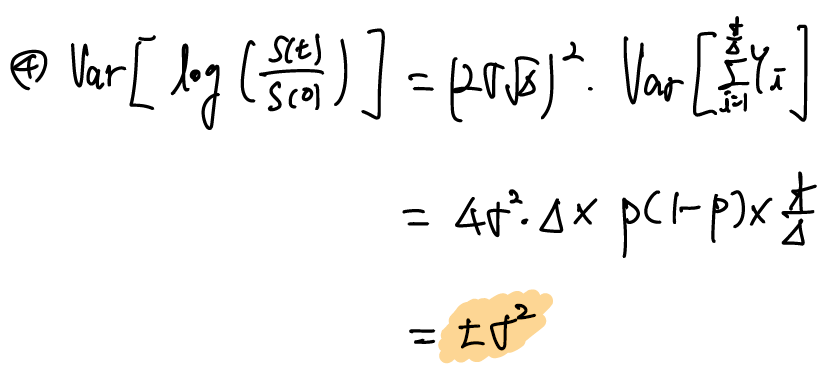
'📈 산업공학 📈 > 금융, 파생상품' 카테고리의 다른 글
| [금융공학] 콜옵션, 풋옵션 이해하기 (0) | 2021.10.19 |
|---|---|
| [경제성공학] 이자율이 실시간으로 계속 변하는 경우 (0) | 2021.10.18 |
| [경제성공학] RoR(Rate of Return)이란? (0) | 2021.10.18 |
| [금융공학] Geometric Brownian Motion 소개 (0) | 2021.10.17 |
| [ 경제성공학 ] Doubling Rule 소개 및 Python으로 간단하게 구현하기 (0) | 2021.09.24 |