[금융공학] Geometric Brownian Motion 소개

1. GBM(Geometric Brownian Motion)이란?

GBM은 주식의 기하학적 브라운 운동을 말하며, 2개의 parameter $\mu$(drift parameter)와 $\sigma$(volatility parameter)를 가진다. 

- $\mu$ (drift parameter) : 주식 가격의 트랜드를 반영하는 변수이다. 기울기를 나타낸다.

- $\sigma$ (volatility parameter) : 주식 가격의 변동성을 반영하는 변수이다. 그래프의 떨리는 정도를 나타낸다.

 

 https://medium.com/the-quant-journey/a-gentle-introduction-to-geometric-brownian-motion-in-finance-68c37ba6f828

 

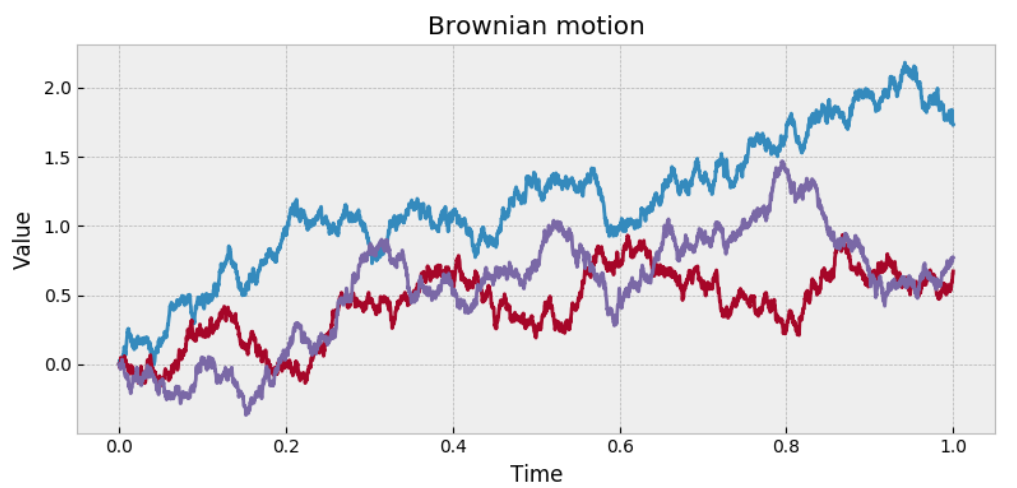
현재 시간을 0이라 하고, $y$시기의 주식 가격을 $S(y)$라고 하자. 

 

변수로 $\frac{S(t+y)}{S(y)}$가 있다고 하자. ($\frac{S(2)}{S(1)}$, $\frac{S(3)}{S(2)}$..., 이들은 각각 다 독립적이다. 서로에게 영향을 주지 않음) 

 

만약 $log \frac{S(y+t)}{S(y)}$ 가 $N(t\mu, t\sigma ^2)$를 따르는 정규분포라면,

 

 $\frac{S(t+y)}{S(y)}$ 는 logNormal 분포이며, 매개변수로 $t\mu$와 $t\sigma$를 가진다. 

그리고 $S(y)$는 매개변수로 $\mu$와 $\sigma$를 가지는 GBM을 따른다!! 

 

 

※ logNormal이란?

임의의 확률변수 Y가 있다고 하자.

만약 $log Y$가 정규분포(Normal Distribution)를 따르고, $\mu$와 $\sigma$를 매개변수로 가진다면,

Y는 lognormal 분포를 따른다.

 

$Y$ ~ $N(e^{\frac{\mu^2+\sigma^2}{2}}, e^{2\mu + \sigma ^2}(e^{\sigma^2}-1))$ (로그정규분포)

$log Y$ ~  $N(\mu, \sigma ^2)$ (정규분포)

 

 

 

2. GBM의 성질

① 미래 주식 가격은 과거 가격에 영향을 받지 않고 오로지 현재 가격 자체에만 영향을 받는다.

② 주식 가격 상승 확률은 현재 가격과 무관하게 상승할 확률이 동일하다. 

예를 들어, A의 현재 주식 가격이 100원이고 B의 현재 주식 가격이 100만원이라면 A 주식 가격이 상승할 확률이 비교적 높다는 것은 자명하다. 하지만 GBM 모형에서는 현재 가격과 무관하게 주식가격이 상승할 확률이 A, B 전부 같다.

 

3. GBM 모형 분석

$\Delta$를 아주 짧은 시간이라고 하자. 

주식가격이 $\Delta$ 시간이 지나고, 오를 확률을 p  내릴 확률을 1-p인 베르누의 확률분포를 따른다고 하자. 그리고 오르는 비율을 u, 내리는 비율을 d라고 가정하자.

상승 비율 u, 하락 비율 d, 오를 확률 p는 아래와 같이 정의한다.

$$u = e^{\sigma \sqrt{\Delta}}$$

$$d = e^{-\sigma \sqrt{\Delta}}$$

$$p = \frac{1}{2}(1 + \frac{\mu}{\sigma}\sqrt{\Delta})$$

 

이 때 $\Delta$가 0으로 수렴하면 u, d는 1로 수렴하고, p는 $\frac{1}{2}$로 수렴한다. 

$\Delta$를 점점 작게 만들게 되면 주식 가격은 주식 가격이 실시간으로 미세하게 진동하는 GBM을 따르게 된다.